O que é interferometro

Interferômetro de Michelson-Morley

      Os interferômetros normalmente podem ser classificados em interferômetros de divisão da frente de onda ou de divisão de amplitude. No interferômetro de divisão da frente onda, partes distintas da frente de onda primária geram ondas secundárias, diretamente ou através de sistemas ópticos, e posteriormente estas ondas secundárias interagem gerando os padrões de interferência. O Interferômetro de fenda dupla de Young é um interferômetro deste tipo. No interferômetro de divisão de amplitudes, a onda primária é dividida em ondas secundárias que possuem a mesma estrutura da onda primária, mas com amplitudes que a somatória não excede à primária. As ondas secundárias propagam por trajetórias distintas e posteriormente interagem e interferem. O interferômetro de Michelson-Morley é um interferômetro desse tipo.

    A base experimental do experimento de Michelson-Morley é composta por uma fonte de luz, dois espelhos, um espelho semi-reflexivo (divisor de feixes) e um anteparo de visualização das franjas, que são disponibilizados conforme Fig 1.

Figura 1 - Representação do interferômetro de Michelson-Morley

O feixe de luz ao ser emitido pela fonte é dividido em dois feixes secundários pelo divisor de feixes, um feixe secundário é dirigido ao espelho A e o outro é dirigido ao espelho B, os dois feixes são refletidos novamente ao divisor de feixes, onde ocorrem novas divisões de feixes. Dois feixes resultantes destas divisões são dirigidos ao anteparo de visualização das franjas formando um feixe composto. No anteparo é possível verificar os padrões de interferência.


Veja o simulador abaixo

As ondas transmitidas e refletidas possuem amplitudes inferiores à onda inicial, portanto diz-se que a amplitude é “dividida”. A visualização dos padrões de interferência somente é possível se a coerência inicial entre as ondas não tiver sido destruída pelo espelho semi-reflexivo e se a trajetória das ondas não for maior do que o comprimento de coerência. Nota-se que a coerência entre os dois feixes é conseguida pela “divisão” de amplitude de um feixe primário. Apesar de ser possível atualmente, com certas restrições, criar padrões de interferência com duas fontes distintas, é mais viável criar feixes coerentes de um feixe primário.  

Uma forma de se compreender a formação dos padrões de interferência no interferômetro de Michelson-Morley é considerar o diagrama abaixo 

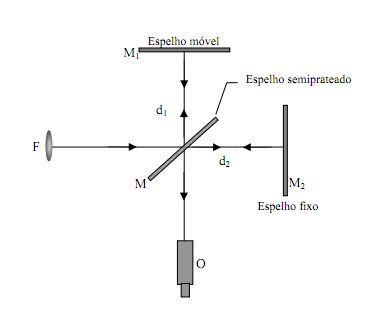
Fig.2: esquema interferometro

Considere que a luz parte da fonte extensa F e incide no espelho semiprateado (M), de espessura desprezível. A luz é então dividida em dois feixes que seguem respectivamente para os espelhos M1 e M2. Estas ondas são refletidos de volta para M onde eles são respectivamente transmitidos e refletidos indo interferir no ponto de observação O.

De M1 temos a esquação da onda associada dada por

E1=A1(sen (wt-a1))   (1)

De M2 temos

E2=A2(sen(wt-a2))   (2)

Em P temos a superposição e a amplitude A será dada por:

A^2=A2^2+A2^2 + 2*A1*A2*cos b           (3)

Onde b é a defasagem existente entre as ondas E1 e E2.

Sendo os feixes coerentes, esta defasagem vai depender do indice de refração e da distancia dos trajetos percorridos

b= K (diferença de trajetos)

b= 2pi/l(d2-d1)                 (4)

onde l representa o comprimento de onda

Teremos um ponto de máximo em O se b=N*2pi

Assim teremos

2*pi/l(d2-d1)=N*2pi

                         (d2-d1)/l=n                         (5)

Se movimentarmos o espelho M1 de uma distancia d o feixe percorre uma distancia 2*d

Vamos considerar que tenhamos uma dada distancia percorrida e um mesmo indice de refração nos trechos d1 e d2.

(d2-d1)= n1l          (6)    (em O um ponto de maximo se N=inteiro)

Se alterarmos a posição do espelho M1 deslocando-o uma distancia igual a d teremos para diferença de trajeto que;

(d2-d1)+2d= n2l                (7)

Subtraindo (7) de (6)

2d= (n2-n1)*l                 (9)

Ou seja , no ponto O, enquanto d variar, o valor de N2 também varia o que significa que o número de máximos varia.

Assim teremos uma variação do numero de máximos igual a

n2-n1=n                (10)

Ou seja obtemos a relação

2d= (n)*l              (11)

Onde n corresponde ao numero de máximos em O que forma obtidos desde a condição inicial (poisção inicial do espelho) até sua posição final d


Veja o simulador abaixo . Varie a posição do espelho e verifique o que ocorre com o padrão de interferência

Simulador do Experimento de Michelson-Morley




Para baixar e executar este aplicativo clique aqui


Assim o procedimento do experimento consiste basicamente em:

1. Alinhar os espelhos de modo a superpor os dois feixes e obter um dado padrão de interferencia.

2. Se o indice de refração é constante o padrão de interferência depende unicamente da distancia d correspondente ao deslocamento do espelho M1

3. Podemos obter o valor do comprimento de onda, ou o valor do deslocamento do espelho, contando o numero de máximos que são obtidos nesta alteração (n)


No experimento proposto, a posição do espelho M1 é alterada atraves do aquecimento de um ferro de solda que por dilatação altera a posição do espelho

Para a contagem do numero de maximos temos um fotosensor (LDR) disposto em uma dada posição da tela.

Nesta 1a etapa o experiemnto é apenas qualitativo, mas pode-se determinar o deslocamento sofrido pelo espelho , considerando como conhecido o comprimento de onda da luz incidente.

Numa 2a etapa pretendemos determinar a temperatura do ferro de solda de modo que será possivel determinar o coeficiente de dilatação linear do material que constitui a ponteira do ferro

Algumas Referencias (na web)

http://www.ifi.unicamp.br/~accosta/roteiros/6/nota%2006.html


http://www.dfi.isep.ipp.pt/uploads/ficheiros/4004.pdf


http://www.dfi.ufms.br/flavio/Cursos/Laboratorio%20Fisica%20Moderna/Michelson_Molrey.p


http://www.ifsc.usp.br/~lavfis/BancoApostilasImagens/ApMichelson/michelson.pdf

http://www.ub.edu/javaoptics/index-en.html (simulador experimento Michelson-Morley)